数状数组

树状数组总结

一、引入背景

• 前缀和数组：能在 O(1) 时间内查询区间和，但修改时需要 O(n) 时间维护。
• 树状数组（Fenwick Tree）：
  • 查询区间和：O(log n)
  • 单点修改：O(log n)
  • 综合时间复杂度：O(n log n) → 适用于 频繁修改 + 区间查询 的场景。

---

二、核心思想

树状数组借鉴了 二进制分解 和 前缀和 的思想，将数组和分别拆分成多个子区间（用 c[i] 存储），形成一个树状结构。 每个 c[i] 管理一段区间，具体由二进制最低位 lowbit(i) 决定。

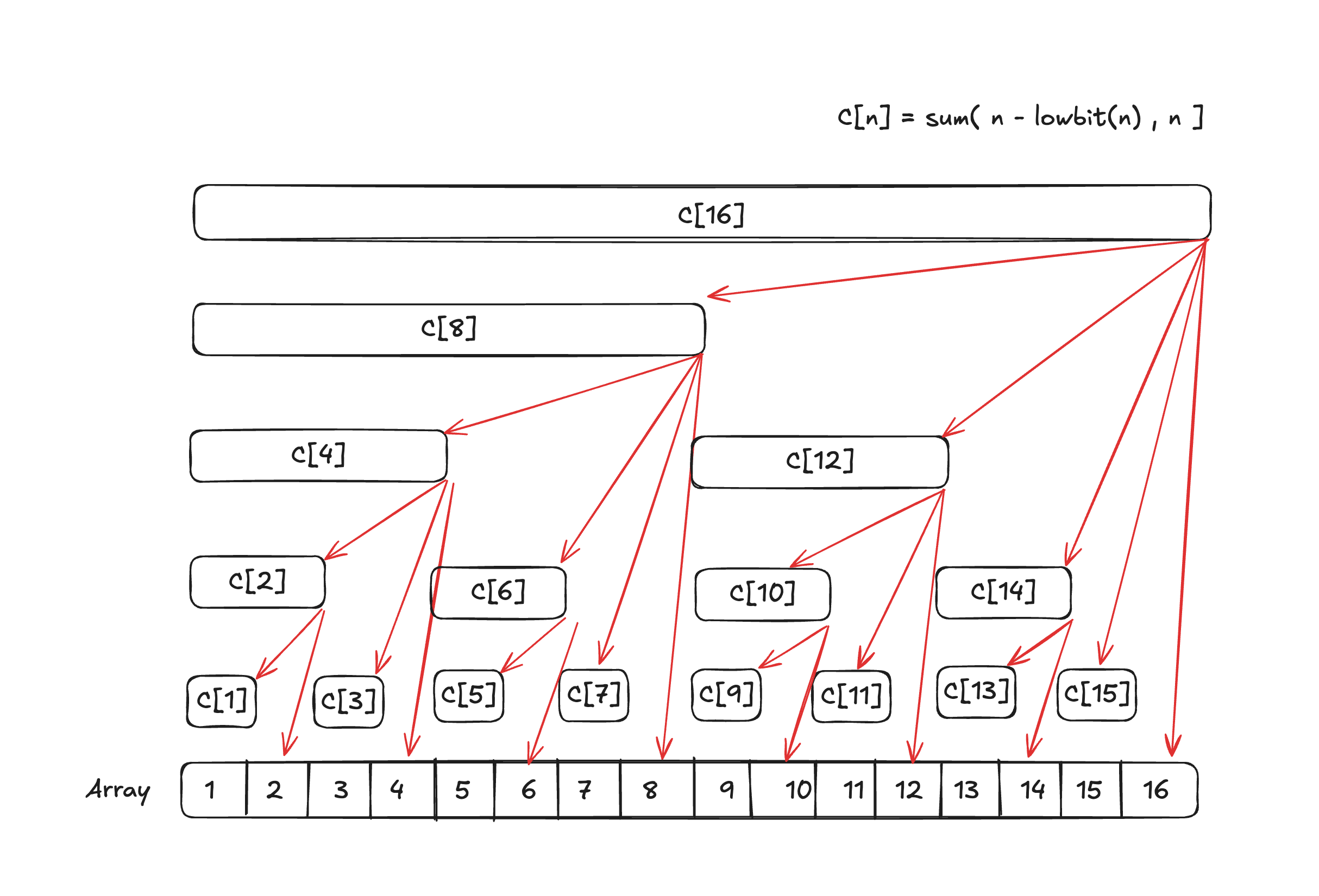
公式：$c[n] = \sum_{k=n-\text{lowbit}(n)+1}^{n} a[k]$

即：c[n] 存储从 n - lowbit(n) + 1 到 n 的数组元素和。

---

三、两个核心操作

1. 求前缀和（父找子）

• 目标：查询数组 [1..n] 的和。

• 方法：不断减去 lowbit，逐步累加。

  sum(n) = c[n] + c[n - lowbit(n)] + c[n - lowbit(n) - lowbit(n - lowbit(n))] + ...

• 图中：箭头从上往下，c[n] 包含更小的子区间。

• 时间复杂度：因为是位运算 所以是O(logn)

---

2. 单点修改更新父节点（子找父）

• 目标：当 a[i] 修改时，更新所有包含 i 的节点 c[j]。

• 方法：不断加上 lowbit，逐步往上更新。

  for (j = i; j <= n; j += lowbit(j)) c[j] += delta

• 即 i 的父节点一定是 i + lowbit(i)，因为它的管理区间更大，能覆盖 i。

• 图中：箭头从下往上，c[i] 往父节点传播。

---

四、为什么 i + lowbit(i) 一定是父节点？

1. 包含性：
   • j = i + lowbit(i)
   • 因为 j - lowbit(j) + 1 ≤ i ≤ j，所以 c[j] 一定覆盖 i。
     • j - lowbit(j) + 1 = i + lowbit(i) - lowbit(j) + 1 —> lowbit(j) > lowbit(i) (因为lowbit(j) 一定比lowbit(i) 高一位或者更多位)—>因此满足 j-lowbit(j) + 1 <= i
2. 最小性：
   • 假设存在 i < k < i+lowbit(i) 也覆盖 i，则 lowbit(k) ≤ lowbit(i)，覆盖范围小于等于 i，无法成为父节点（我们子找父一定是往上找，一直找覆盖范围比自己大的）。
   • 因此 i+lowbit(i) 是最小的父节点。

---

五、总结一句话

**树状数组是利用二进制分解思想维护的前缀和数据结构，支持 O(log n) 的单点修改与区间查询，核心操作就是 lowbit 控制的父子关系：前缀和时“父找子”，更新时“子找父”。